TL;DR
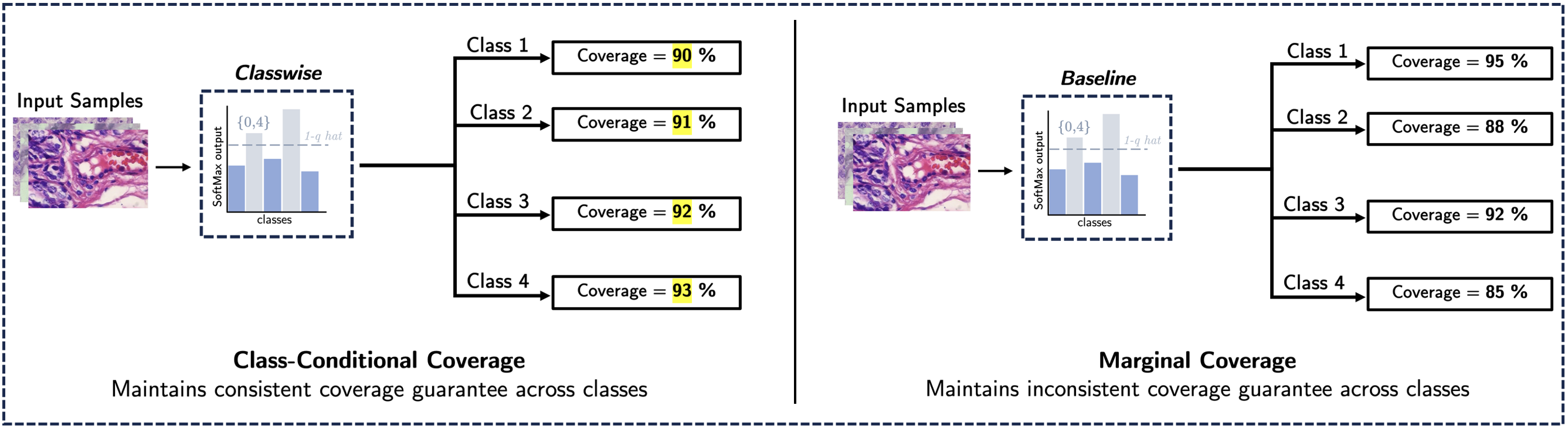
Standard CP methods are focused on providing marginal coverage guarantees, which can lead to inconsistent coverage guarantees across different classes leading to misdiagnosis. Working upon this, we propose a Classwise CP method that achieves a stricter coverage guarantee across all classes i.e class conditional coverage in a pathological workflow. Our results demonstrate a significant reduction in the average class coverage gap compared to the Baseline CP method.
Abstract
Conformal Prediction (CP) is an uncertainty quantification framework that provides prediction sets with a user-specified probability to include the true class in the prediction set. This guarantee on the user-specified probability is known as marginal coverage. Marginal coverage refers to the probability that the true label is included in the prediction set, averaged over all test samples. However, this can lead to inconsistent coverage guarantees across different classes, constraining its suitability for high-stakes applications such as pathological workflows. This study implements a Classwise CP method applied to two cancer datasets to achieve class conditional coverage which ensures that each class has a user-specified probability of being included in the prediction set when it is the true label. Our results demonstrate the effectiveness of this approach through a significant reduction in the average class coverage gap compared to the Baseline CP method.
Methodology
After test and calibration split, we calculate a separate threshold \( \hat{q}^k \) for each class within the calibration data. Now for each test data point, we generate prediction sets as: \( C(x)_k = \{ y: s(x, y) \geq 1 - \hat{q}^k \} \) for each class based on their respective thresholds \( \hat{q}^k \). The final prediction set for each test data point is obtained by taking the union of the prediction sets across all classes: \( C(x) = \bigcup_{k \in \mathcal{K}} C(x)_k \), where \( \mathcal{K} \) denotes all classes. Finally, we assess the class-wise coverage guarantee for each class by comparing the Baseline and Classwise CP methods, using the average class coverage gap (CovGap) metric, which is defined as:
where \( \hat{c}_k \) is the empirical class-conditional coverage of class \( k \). For this study, we employed DieT as the underlying model for CP for its superior performance on CRIC and BreakHis datasets.
Results
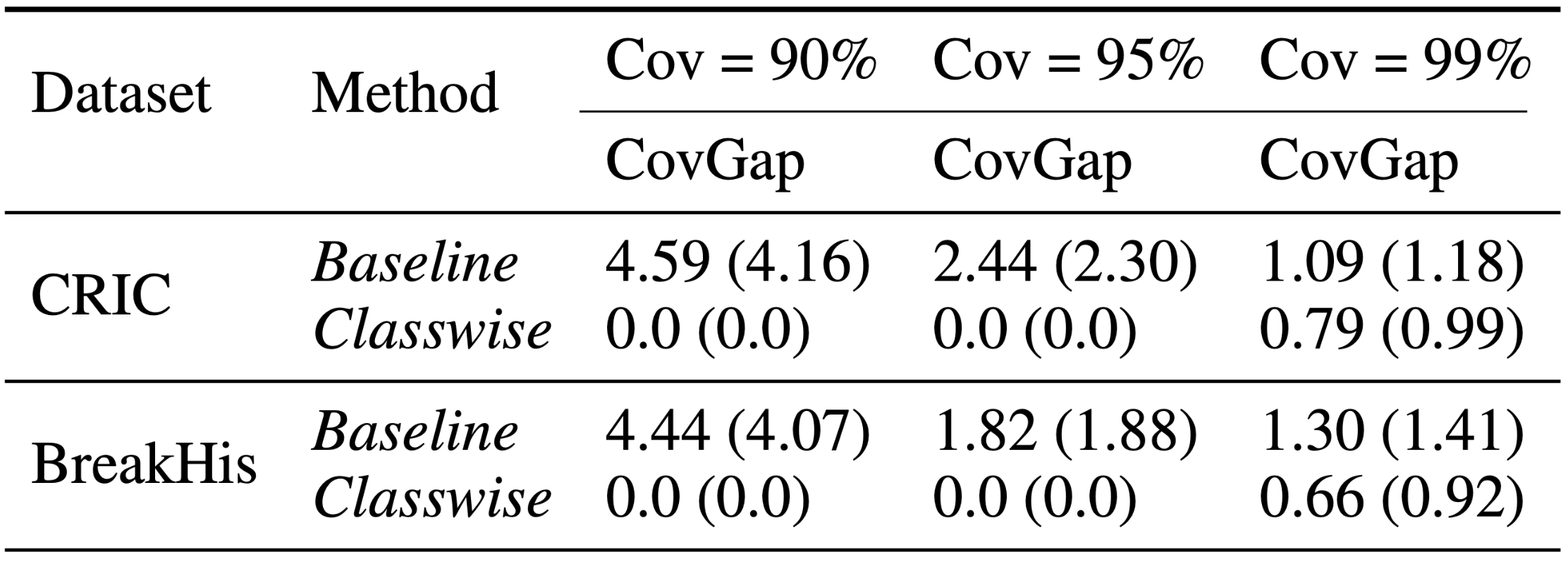
Our results demonstrate that the Classwise approach effectively minimizes the average class coverage gap (CovGap), with reductions ranging from 27.52% to 100% across various datasets and coverages. These results can enhance diagnostic precision and contribute to improved patient care outcomes in pathological workflows.